"Quantum Numbers: Building Blocks of Atomic Structure"

  Quantum Numbers

Quantum Numbers 

Here you will learn about quantum numbers that are used to describe the electrons present in the atom, the difference between shell and subshell, the concept of the orbital, and the rules for filling orbitals.

The physical features of nature at the size of atoms and subatomic particles are described by the fundamental physics theory known as quantum mechanics. It serves as the theoretical cornerstone for all branches of quantum physics, including "quantum information science, quantum technology, quantum field theory, and quantum chemistry".

The wave functions (Ψ) that result from solving the Schrödinger equation (HΨ= EΨ) describe the likelihood of finding electrons at different energy levels within an atom.

The term "atomic orbital" refers to a wave function for an electron in an atom that specifies an area of space where there is a good chance of finding the electron. An electron's transition from a wave pattern with one energy to a wave pattern with another energy causes energy shifts within an atom "(usually accompanied by the absorption or emission of a photon of light)".

Four separate quantum numbers are used to characterize each electron in an atom.

These are

1. principal Quantum number

2.Azimuthal Quantum number

3. Magnetic Quantum number

4. Spin Quantum number

The Bohr model was a one-dimensional representation of the atom's electron dispersion that used a single quantum number. The size of the orbit, which is defined by the n quantum number, was the only piece of information that mattered. The electron was able to occupy three dimensions thanks to Schrodinger’s model. As a result, describing the orbitals in which electrons can be found requires three coordinates or three quantum numbers.

The principal (n), angular (l), and magnetic (m) quantum numbers are the three coordinates that result from Schrodinger's wave equations. The size, form, and spatial orientation of the orbitals are all described by these quantum numbers.

Now explain one by one

1. principal Quantum number (n)

Given by Bohr, used to measure the distance of electrons from the nucleus

The letter "n" stands for the principal quantum number. They identify the atom's principal electron shell. A larger value of the primary quantum number signifies a greater distance between the electron and the nucleus since it describes the most likely distance between the two (which, in turn, implies a greater atomic size).

Any integer with a positive value equal to or greater than one can have the value of the principal quantum number. The lowest energy level (also known as the ground state) of an electron is represented by the value n=1, which stands for the innermost electron shell of an atom.

Energy is released when electrons jump to a lower energy level and the value of n also decreases, similarly the value of n increases when an electron moves from a lower to a higher energy level.

The value of n spans from 1 to the atom's outermost electron or the shell, thus

n = 1, 2, …

Principal Quantum Number

 The total number of electrons in the shell can be known by using the formula that is 2n²

Total number of orbitals in orbit = n²

^{Total number of subshell in an orbit = n}

Angular momentum finds out by formula = nh/2Π

2.Azimuthal Quantum number (ℓ)

Given by Arnold Sommerfeld uses the Bohr atomic model, used to describe the shape of subshells.

The orientation of an orbital is described by its azimuthal quantum number, also known as orbital angular momentum. Its value is equal to the total number of angular nodes in the orbital, and it is represented by the letter " ℓ".

ℓ = 0,1,2,3….

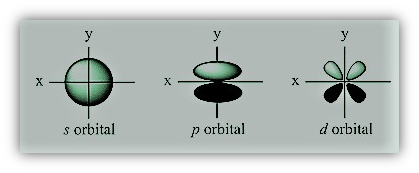
A value of the azimuthal quantum number can represent a different-shaped s, p, d, or f subshell.

The orbital's form is described by the angular quantum number (ℓ). The best descriptions for the forms of orbitals are spherical (ℓ = 0), polar (ℓ = 1), or cloverleaf (ℓ = 2). As the angular quantum number increases, they can even assume more intricate shapes.

 

Total number of orbital in a subshell = (2l+1)

Total number of electrons in a subshell = 2(2l+1)

 

3. Magnetic Quantum number (m_ℓ)

Given by Lande to explain the Zeeman effect and stark effect, used to indicate the direction of electron density.

The magnetic quantum number determines the total number of orbitals in the shell as well as their configuration. The letter "m_ℓ" stands for it. This value produces the projection of the orbital's angular momentum along a specified axis.

The azimuthal quantum number, also known as the orbital angular momentum quantum number, determines the value of the magnetic quantum number. The range of the value of ml for a given value of l is from -l to +l.

Maximum no. of electrons in a subshell = 2 with opposite spin

4. Spin Quantum number (m_s)

Discovered by Unlenbeck and Goudsmit, used to find the spin of an electron in an atom.

The values of n, l, and ml have no effect on the electron spin quantum number. The symbol m_s is used to represent the value of this number, which reveals the direction in which the electron is spinning.

The value of m_s provides information on the spin direction of the electron. The electron spin quantum number ranges between +1 and -1.

The ability of an atom to generate a magnetic field depends on the value of the electron spin quantum number. It is possible to generalize the value of m_s to ±1/2.

Determing the number of Electrons, Shells, Subshell, Orbitals and relationship among Quantum Numbers :

Here are some formulas and relationships related to quantum numbers:

1. Maximum number of electrons per energy level: 

The maximum number of electrons that can occupy a given energy level (shell) is given by the formula 2n², where n is the principal quantum number.

2. Number of subshells in an energy level: 

The number of subshells within an energy level is equal to the value of the principal quantum number. For example, if n=3, there are three subshells (l=0,1,2) within the third energy level.

3. Maximum number of electrons in a subshell:

 The maximum number of electrons that can exist within a subshell is given by the formula 2(2l+1), where l is the angular momentum quantum number. For example, in the s subshell (l=0), there can be a maximum of 2(2*0+1) = 2 electrons.

4. Maximum number of orbitals in an orbit:

The formula to calculate the number of orbitals in an energy level (orbit) is given by n^2, where n is the principal quantum number.

For example, if the principal quantum number is n=3, the number of orbitals in the third energy level would be 3^2 = 9 orbitals. One of S, three p-orbitals (px, py, pz) and five d-orbitals. These orbitals are designated as dxy, dxz, dyz, dx^2-y^2, and dz^2.

Similarly, if n=4, the number of orbitals in the fourth energy level would be 4^2 = 16 orbitals. 1-s, 3-p(x,y,z),5-d as given above and seven f-orbitals. These orbitals are designated as fy3x2-y2, fxyz, fxz^2, fyz^2, fz^3, fx^2-y^2z^2, and fx(x^2-3y^2). 

5. Relationship between n and l:

The value of the angular momentum quantum number (l) can range from 0 to (n-1), where n is the principal quantum number. For example, if n=3, l can be 0, 1, or 2.

6. Relationship between l and ml: 

For a given value of l, the magnetic quantum number (ml) can take any value from -l to +l. For example, if l=2, ml can be -2, -1, 0, 1, or 2.

7. Relationship between n, l, and ml: 

In combination, the principal quantum number (n), angular momentum quantum number (l), and magnetic quantum number (ml) uniquely define each orbital within an atom.

These formulas and relationships help in determining the maximum number of electrons in energy levels and subshells, as well as understanding the allowed values for quantum numbers in atoms.

Difference between shell and subshell:

A shell is formed by orbitals with the same principal quantum number value. A shell's orbitals are separated into subshells with the same angular quantum number. A two-character identifier, such as 2p or 4f, is used by chemists to identify the shell and subshell that an orbital resides. The shell is indicated by the first character (n = 2 or n = 4). The subshell is designated by the second character.

                           

s (subshell)	ℓ =	0 (shell)
p (subshell)	ℓ =	1 (shell)
d (subshell)	ℓ =	2 (shell)
f (subshell)	ℓ =	3 (shell)

 

Concept of Orbitals:

The parts of the atom where finding electrons is most likely to occur are called electronic orbitals.

The number of possible values the magnetic quantum number, ml, can take on is equal to the number of orbitals in a subshell. The formula 2l +1 is useful for calculating the number of orbitals in a subshell. This equation gives you the range of possible values for ml in a certain orbital rather than the actual value of ml. For instance, if l=2 and ml can have one of five values (-1, -2, 0, or +1, +2), 2l+1 will have a value of 5, and there will be three distinct orbitals. The orbitals are given names based on the subshells they are located in.

For example, if they are present in s subshell they are called as s-orbital.

Rules for filling of orbitals (Electronic configuration)

Aufbau principle:

Fill up the electrons in the increasing order of energy in a subshell.

(n+l) rule:

The low value of subshell (n+l) fills first but if two or more subshell has the same value of n+l then fills the one first that have a low value of the principal quantum number(n).

Pauli exclusion principle:

“No two electrons in an atom have the same value as all four quantum numbers.” The maximum number of electrons that can occupy an orbital is two, and they must have opposite spins. Electrons have what are known as "opposing spins," where some spin up and others spin down. The electrons are kept apart as a result of this.

Hund’s rule:

When the electrons fill the orbitals, each one starts out with one electron. The same spin characterizes each unpaired electron. The occupation is then finished by a second electron with the opposite spin.